1. Introduction
When ordering crystals for oscillators that are to operate at a frequency f, e.g. 32.768 kHz or 20 MHz, it is usually not sufficient to specify the frequency of operation alone. While the crystals will oscillate at a frequency near their series resonant frequency, the actual frequency of oscillation is usually slightly different from this frequency (being slightly higher in “parallel resonant circuits”).1
So, suppose you have a crystal oscillator circuit and you want to purchase crystals such that when placed in this circuit the oscillation frequency is f. What do you need to tell the crystal manufacturer to accomplish this? Do you need to send a schematic of the oscillator design with all the associated details of its design, e.g. choice of capacitors, resistors, active elements, and strays associated with the layout? Fortunately, the answer is no. In addition to the frequency f, all that is needed is a single number, the load capacitance CL .
2. What is CL ?
Suppose your crystal oscillator operates at the desired frequency f. At that frequency, the crystal has complex impedance Z, and for the purposes of frequency of operation, this is the only property of the crystal that matters. Therefore, to make your oscillator operate at the frequency f, you need crystals that have impedance Z at the frequency f. So, at worst, all you need to specify is a single complex number Z = R+jX. In fact, it is even simpler than this.
While in principal one should specify the crystal resistance R at the frequency f, usually the crystal-to- crystal variation in R and the oscillator’s sensitivity to this variation are sufficiently low that a specification of R is not necessary. This is not to say that the crystal resistance has no effect; it does. We shall discuss this further in Section 4.
So, that leaves a single value to specify: The crystal reactance X at f. So, one could specify a crystal having a reactance of 400 ? at 20 MHz. Instead,however, this is normally done by specifying acapacitance C L and equating.

where we have set ω = 2πf. Physically, at this frequency, the impedance of the series combination of the crystal and a capacitance C L has zero phase (equivalently, has zero reactance or is purely resistive). See Figure 1. To see this, consider

where the second step follows by Equation (1) and the fact that the reactance of a capacitance C is -1/( ωC).
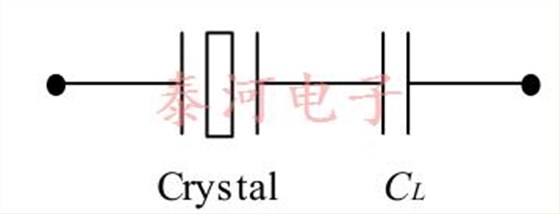
Figure 1—This series combination has zero-phase impedance at a frequency where the crystal has load capacitance CL
So, the task of assuring proper oscillation frequency is the task of providing components (crystals in this case) that, at the specified frequency, have the required reactance, which is stated in terms of a capacitance CL by Equation (1).2For example, instead of specifyingcrystals having a reactance of 400 ? at 20 MHz, we specify crystals having a load capacitanceof 20 pF at 20 MHz, or more normally, we specify that the crystal frequency be 20 MHz at aload capacitance of 20 pF.
In “parallel resonant circuits,” CL is positive, typically being between 5 pF and 40 pF. In this case the crystal operates in that narrow frequency band between the crystal’s series and parallel resonant frequencies (F s and F p , respectively).
While a truly “series resonant circuit” does not have aload capacitance associated with it [or perhaps aninfinite value by Equation (1)], most “series resonantcircuits” actually operate slightly off of the seriesresonant frequency and therefore do have a finiteload capacitance (that can be positive or negative).However, if this offset is small and specifying a loadcapacitance is not desired, it can either be ignored orhandled by a slight offset in the specified frequency f.
As we shall see in Section 4, both the oscillator andthe crystal determine C L . However, the crystal’s roleis rather weak in that in the limit of zero resistance,the crystal plays no role at all in determining C L . Inthis limiting case, it makes sense to refer to C L as theoscillator load capacitance as it is determinedentirely by the oscillator. However, when it comestime to order crystals, one specifies crystals havingfrequency f at a load capacitance C L , i.e. it is acondition on the crystal’s frequency. Because of this,it would be reasonable to refer to C L as the crystalload capacitance. For the sake of argument, wesimply avoid the issue and use the term loadcapacitance.
注释:1> When ordering crystals for series resonant operation,instead of specifying a value for C L , be sure to state that the frequency f refers to the series-resonant frequency, F s .
2>This is not to say that all aspects of frequency determination are tied to this single number. For example,other aspects of the crystal and oscillator determine whether the correct mode of oscillation is selected and the system’s frequency stability (short and long term).
3. Defining F L at C L
We now take Equation (1) as our defining relation forwhat we mean by a crystal having a given frequencyat a given load capacitance.
Definition: A crystal has frequency F L at a loadcapacitance C L when the reactance X of the crystal atfrequency F L is given by Equation (1), where nowω = 2πF L .
Recall that, around a given mode, the reactance of acrystal increases from negative values, through zeroat series resonance, to large positive values nearparallel resonance where it rapidly decreases to largenegative values, and then again it increases towardszero. (See Reference [1].) By excluding a regionaround parallel resonance, we have a singlefrequency for each value of reactance. In this way,we can associate a frequency F L given a value of C L .So, positive values of C L correspond to a frequencybetween series and parallel resonance. Largenegative values of C L , correspond to a frequencybelow series resonance while smaller negative valuescorrespond to frequencies above parallel resonance.(See Equation (3) below.)
3.1. The crystal frequency equationSo, how much does the frequency of oscillationdepend on the load capacitance C L ? We can answerthis question by determining how the crystalfrequency F L depends on the crystal load capacitanceCL . One can show that to a very good approximationthat
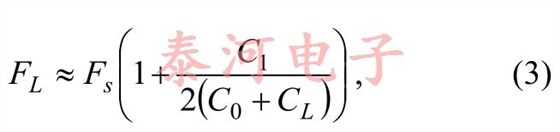
where C 1 and C 0 are the motional and staticcapacitances of the crystal, respectively. (SeeReference [1] for a derivation and discussion of thisrelation.) For the purposes of this note, we shall referto Equation (3) as the crystal frequency equation.
This shows the dependence of a crystal oscillator’soperational frequency on its load capacitance and itsdependence on the crystal itself. In particular, thefractional frequency change when changing the loadcapacitance from C L1 to C L2 is given to goodapproximation by
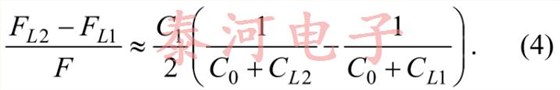
3.2. Trim sensitivity
Equation (3) gives the dependence of operatingfrequency F L on the load capacitance C L . Thenegative fractional rate of change of the frequencywith C L is known as the trim sensitivity, TS. UsingEquation (3), this is approximately
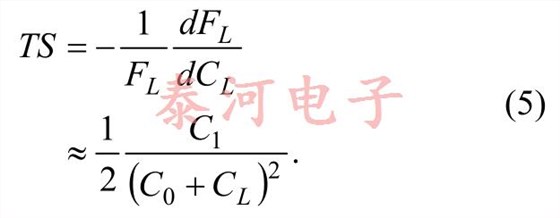
From this we see that the crystal is more sensitive togiven change in C L at lower values of C L .
4. But what determines C L ?
Consider the simple Pierce oscillator consisting of acrystal, an amplifier, and gate and drain capacitors asshown in Figure 2.
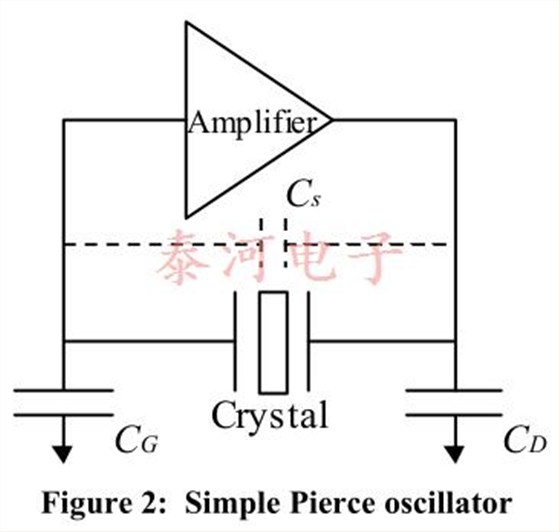
There are at least three stray capacitances that mustbe considered in trying to calculate the loadcapacitance of the Pierce oscillator circuit.
1. An added capacitance from the input of theamplifier to ground. Sources for this could bethe amplifier itself and trace capacitance toground. As this capacitance is in parallel withC G , we can simply absorb this into our definitionof C G . (That is C G is the capacitance of thecapacitor to ground plus any additionalcapacitance to ground on this side of theamplifier.)
2. An added capacitance from the output of theamplifier to ground. Sources for this could bethe amplifier itself and trace capacitance toground. As this capacitance is in parallel withC D , we can simply absorb this into our definitionof C D . (That is C D is the capacitance of thecapacitor to ground plus any additionalcapacitance to ground on this side of theamplifier.)
3. A stray capacitance C s shunting the crystal asshown in Figure 2.
Redefining C G and C D as discussed above, it thenfollows [2] that one of the conditions for oscillation is
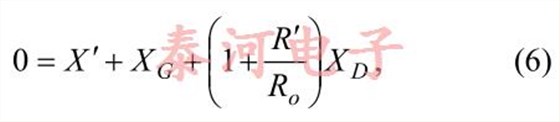
Where

is the impedance of the parallel combination of thecrystal and the capacitance C s and R o is the outputresistance of the amplifier.
It can be shown that the crystal resistance R as afunction of load capacitance C L is givenapproximately by (provided C L is not too small)
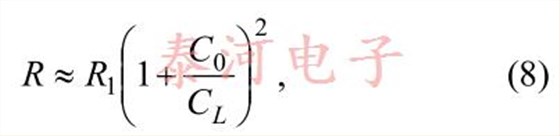
where R 1 is the motional resistance of the crystal [1].It then follows that (provided C L – C s is not toosmall)
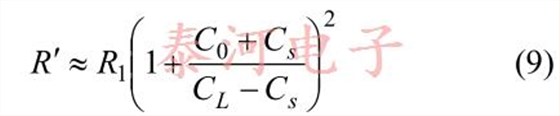
And
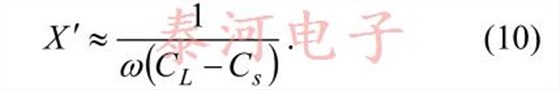
With these results, Equation (6) gives the followingequation for C L
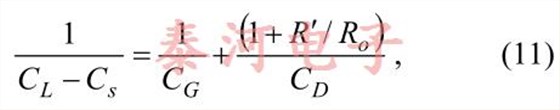
where R ′ is approximated by Equation (9). Note thatthe equation for C L is actually a bit more complicatedthan it might seem at first as R ′ depends upon on C L.It can be seen that C L decreases as R 1 increases, andso by Equation (3), the frequency of operationincreases with crystal resistance. So, the loadcapacitance does have a dependence on the crystalitself. But as we have mentioned previously, thevariation in crystal resistance and resulting sensitivityto this variation is usually sufficiently low that thedependence can be ignored. (In this case, a nominalvalue for crystal resistance is used in calculating C L .)
However, sometimes the resistance effect cannot be ignored. Two crystals tuned so that both have exactly the same frequency at a given load capacitance C L can oscillate at different frequencies in the same oscillator if their resistances differ. This slight difference leads to an increase in the observed system frequency variation above that due to crystal frequency calibration errors and the board-to-board component variation.
Note that in the case of zero crystal resistance (or at least negligible compared to the output resistance Ro of the amplifier), Equation (11) gives
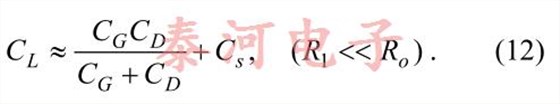
So, in this case, the load capacitance is the straycapacitance shunting the crystal plus the seriescapacitance of the two capacitances on each side ofthe crystal to ground.
5. Measuring CL
While in principal one could calculate C L from thecircuit design, an easier method is simply to measureC L . This is also more reliable since it does not relyon the oscillator circuit model, takes into account thestrays associated the layout (which can be difficult toestimate), and it takes into account the effect ofcrystal resistance. Here are two methods formeasuring C L .
5.1 Method 1
This method requires an impedance analyzer, butdoes not require knowledge of the crystal parametersand is independent of the crystal model.
1. Get a crystal that is similar to those that will beordered, i.e. having similar frequency andresistance.
2. Place this crystal in the oscillator and measurethe frequency of operation F L . In placing thecrystal into the circuit, be careful not to damageit or do anything to cause undue frequency shifts.(If soldered in place, allow it to cool down toroom temperature.) A good technique thatavoids soldering is simply to press the crystalonto the board’s solder pads using, for example,the eraser end of a pencil and observe theoscillation frequency. Just be careful that thecrystal makes full contact with the board. Thesystem can still oscillate at a somewhat higherfrequency without the crystal making full contactwith the board.
3. Using an impedance analyzer, measure thereactance X of the crystal at the frequency F Ldetermined in Step 2.
4. Calculate C L using Equation (1) and themeasured values for F L ( ω = 2πF L ) and X at F L .
5.2 Method 2
This method is dependent upon the four-parametercrystal model and requires knowledge of theseparameters (through your own measurement or asprovided by the crystal manufacturer).
1. Get a crystal that is similar to those that will beordered, i.e. having similar frequency andresistance.
2. Characterize this crystal. In particular measureits series frequency Fs , motional capacitance C1,and static capacitance C0.
3. Place this crystal in the oscillator and measurethe frequency of operation F L (as in Method 1,Step 2.)
4. Calculate C L using Equation (3) and themeasured values for F L , F s , C 1 , and C 0 .
It is recommended that either procedure be followedwith at least 3 crystals. When done properly, thistechnique often gives values for C L that are consistentto about 0.1 pF. Further confidence in the finalresults can be found by repeating the procedure for anumber of boards to estimate the board-to-boardvariation of C L .
Note that in the above, F L does not have to beprecisely the desired oscillation frequency f. That is,the calculated value for C L is not a strong function ofthe oscillation frequency since normally only thecrystal is strongly frequency dependent. If, for somereason, the oscillator does have strong frequencydependent elements, then using this procedure wouldbe quite difficult.
6. Do I really need to specify a value for CL ?
There are at least three cases where a specification ofC L is not necessary:
1. You intend to operate the crystals at their series-resonant frequency.
2. You can tolerate large errors in frequency (on theorder of 0.1% or more).
3. The load capacitance of your circuit issufficiently near the standard value (see crystaldata sheet) that the frequency difference istolerable. This difference can be calculated withEquation (4).
If your application does not meet one of the threeconditions above, you should strongly considerestimating the load capacitance of your oscillator anduse this value in specifying your crystals.

 1XTW32768PAA,DSB321SDN,32.768M温补晶振
1XTW32768PAA,DSB321SDN,32.768M温补晶振 1XXD32000PBA
1XXD32000PBA 1XXB32000PAA,DSB221SDN,2520 32M温补晶振
1XXB32000PAA,DSB221SDN,2520 32M温补晶振


