
-
Abracon艾博康ASG2-D压控晶振,ASG2-D-V-A-120.000MHZ低抖动晶振
Abracon艾博康ASG2-D压控晶振,ASG2-D-V-A-120.000MHZ低抖动晶振,AbraconCrystal艾博康晶振,美国进口晶振,ASG2-D系列是一款小体积晶振尺寸2.5x2.0x1.0mm晶振,六脚贴片晶振,VCXO晶振,ASG2-D-V-A-320.000MHZ压控晶体振荡器,ASG2-D-V-B-120.000MHZ-T有源晶振,ASG2-D-V-B-698.812334MHZ石英晶振,贴片晶振,+2.5V或+3.3V操作,-40°C至+85°C标准操作温度范围,陶瓷SMT包交货时间短,具有超小型,轻薄型,低抖动,低功耗,低电源电压,低耗能,低损耗,低电平,低相位噪声等特点,应用于网络,超声波,WiMax/WLAN,计算锁相环,直接数字合成(DDS)DSL/ADSL,础终端统计,无线蓝牙模块,物联网,GPS定位,汽车导航等应用。更多 +

-
TXC晶振,温补晶振,7Z晶振,7Z38471001晶振
VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等,VC-TCXO应用:智能手机晶体,无线基站,精密仪器,GPS卫星,汽车应用等, 晶体滤波器应用,无线收发器,智能手机,无线网络发射,GPS定位等等,汽车产业、消费性电子、信息产业、通信产业与通信基础产业.更多 +

-
TXC晶振,差分晶振,7J晶振,大体积微分输出贴片晶振
VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等.VC-TCXO应用:智能手机晶体,无线基站,精密仪器,GPS卫星,汽车应用等. 晶体滤波器应用,无线收发器,智能手机,无线网络发射,GPS全球定位等等.汽车产业、消费性电子、信息产业、通信产业与通信基础产业.更多 +

-
爱普生晶振,压控晶振,VG-4231CB晶振,X1G0028610007晶振
crystal,石英晶振应用:数码相机,无线通讯,计算机,接口卡,电话,传呼机,遥控器,全球定位系,MP3,MP4,MP5数码产品系列。石英振荡器,爱普生OSC晶振应用:无线通信,智能手机,平板笔记本,计算机,全球GPS定位系统,WLAN网络产品等.VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等更多 +

-
西铁城晶振,贴片晶振,CSX-750PB晶振,ROHS规范有源晶振
VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等,VC-TCXO应用:智能手机晶体,无线基站,精密仪器,GPS卫星,汽车应用等,晶体滤波器应用,无线收发器,智能手机,无线网络发射,GPS全球定位等等,汽车产业、消费性电子、信息产业、通信产业与通信基础产业。更多 +
-
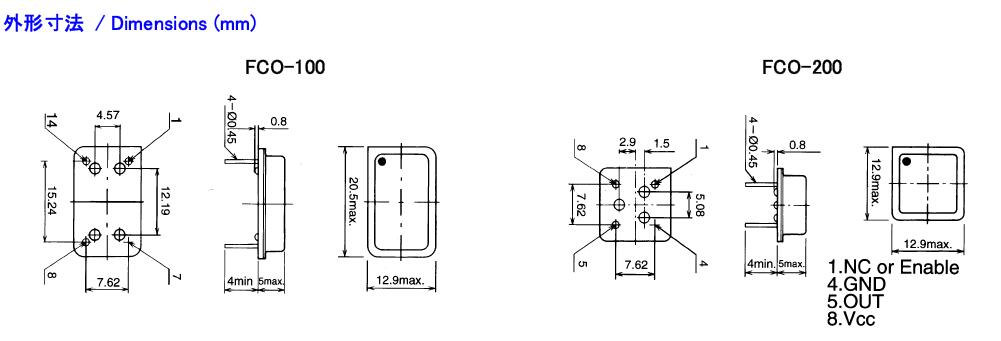
Fujicom晶振,石英晶振,FCO-200晶振,日本进口插件晶振
VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等更多 +
符合RoHS/无铅。

-
Cardinal晶振,石英晶振,CC137晶振,三态控制晶振
更多 +VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等
符合RoHS/无铅。

-
CRYSTEK晶振,贴片晶振,CVS575S-500.000晶振,500MHZ压电控制时钟振荡器
更多 +VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等
符合RoHS/无铅。

-
MERCURY晶振,石英晶振,M14S晶振,DIP温补晶振
VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等更多 +
符合RoHS/无铅。

-
Frequency晶振,贴片晶振,FTL1晶振,普通有源晶振
更多 +VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等
符合RoHS/无铅。
-
Frequency晶振,贴片晶振,FTVC1晶振,低相位噪音VCXO晶振
VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等更多 +

-
Golledge晶振,贴片晶振,GXO-2201G晶振,GXO-2201J晶振,GXO-2201L晶振
更多 +
VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等

-
瑞康晶振,贴片晶振,RXG1490L晶振,LVPECL输出晶振
更多 +VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等

-
京瓷晶振,贴片晶振,FXO-32F晶振,7050普通有源晶振,FXO-32FL晶振
更多 +VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等
符合RoHS/无铅。

-
ABRACON晶振,石英晶振,ACHL晶振,DIP时钟晶振
更多 +VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等
符合RoHS/无铅。

-
京瓷晶振,贴片晶振,KC7050A-C2晶振,KC7050A125.000C20E00晶振
更多 +VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等
符合RoHS/无铅。

-
IDT晶振,贴片晶振,8N4DV85晶振,LVDS输出石英振荡器
更多 +VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等

-
泰艺晶振,贴片晶振,VT晶振,VTEUMCJANF-25.000000晶振
更多 +VCXO是指这款晶体产品控制功能只有单压控也就是电压控制功能,产品本身频率精度可以随着电压搞定起伏来自动调整频率,使产品永远控制在一定的频率范围,压控晶振(VCXO)压控石英晶体振荡器基本解决方案,PECL输出,输出频率60 MHz到200 MHz之间,出色的低相位噪声和抖动,三态功能,应用:SDH/ SONET,以太网,基站,笔记本晶振应用, VCXO,压控晶体应用:调制解调器,ADSL网络控制器,无线基站,程控交换设备智能手机,笔记本晶振等
- [行业新闻]ECS-250-12-33QZ-ADS-TR适合高冲击和高振动环境的理想选择2023年02月15日 08:47
- ECS晶振推出超小型加固型ECX-33QZ紧凑型SMD石英晶体,小体积尺寸采用3.2x2.5x0.8毫米(LWH)四焊盘工业标准陶瓷封装,石英晶体谐振器,这些晶体的坚固设计利用了额外的内部粘合点,使ECS-250-12-33QZ-ADS-TR适合高冲击和高振动环境的理想选择,如汽车和轮胎压力监测系统(TPMS)的应用。
- 阅读(743)
- [技术支持]What is frequency at load capacitance?2019年04月16日 10:07
1. Introduction
When ordering crystals for oscillators that are to operate at a frequency f, e.g. 32.768 kHz or 20 MHz, it is usually not sufficient to specify the frequency of operation alone. While the crystals will oscillate at a frequency near their series resonant frequency, the actual frequency of oscillation is usually slightly different from this frequency (being slightly higher in “parallel resonant circuits”).1
So, suppose you have a crystal oscillator circuit and you want to purchase crystals such that when placed in this circuit the oscillation frequency is f. What do you need to tell the crystal manufacturer to accomplish this? Do you need to send a schematic of the oscillator design with all the associated details of its design, e.g. choice of capacitors, resistors, active elements, and strays associated with the layout? Fortunately, the answer is no. In addition to the frequency f, all that is needed is a single number, the load capacitance CL .
2. What is CL ?
Suppose your crystal oscillator operates at the desired frequency f. At that frequency, the crystal has complex impedance Z, and for the purposes of frequency of operation, this is the only property of the crystal that matters. Therefore, to make your oscillator operate at the frequency f, you need crystals that have impedance Z at the frequency f. So, at worst, all you need to specify is a single complex number Z = R+jX. In fact, it is even simpler than this.
While in principal one should specify the crystal resistance R at the frequency f, usually the crystal-to- crystal variation in R and the oscillator’s sensitivity to this variation are sufficiently low that a specification of R is not necessary. This is not to say that the crystal resistance has no effect; it does. We shall discuss this further in Section 4.
So, that leaves a single value to specify: The crystal reactance X at f. So, one could specify a crystal having a reactance of 400 ? at 20 MHz. Instead,however, this is normally done by specifying a capacitance C L and equating.
where we have set ω = 2πf. Physically, at this frequency, the impedance of the series combination of the crystal and a capacitance C L has zero phase (equivalently, has zero reactance or is purely resistive). See Figure 1. To see this, consider
where the second step follows by Equation (1) and the fact that the reactance of a capacitance C is -1/( ωC).
Figure 1—This series combination has zero-phase impedance at a frequency where the crystal has load capacitance CL
So, the task of assuring proper oscillation frequency is the task of providing components (crystals in this case) that, at the specified frequency, have the required reactance, which is stated in terms of a capacitance CL by Equation (1).2 For example, instead of specifying crystals having a reactance of 400 ? at 20 MHz, we specify crystals having a load capacitance of 20 pF at 20 MHz, or more normally, we specify that the crystal frequency be 20 MHz at a load capacitance of 20 pF.
In “parallel resonant circuits,” CL is positive, typically being between 5 pF and 40 pF. In this case the crystal operates in that narrow frequency band between the crystal’s series and parallel resonant frequencies (F s and F p , respectively).
While a truly “series resonant circuit” does not have a load capacitance associated with it [or perhaps an infinite value by Equation (1)], most “series resonant circuits” actually operate slightly off of the series resonant frequency and therefore do have a finite load capacitance (that can be positive or negative).However, if this offset is small and specifying a load capacitance is not desired, it can either be ignored or handled by a slight offset in the specified frequency f.
As we shall see in Section 4, both the oscillator and the crystal determine C L . However, the crystal’s role is rather weak in that in the limit of zero resistance,the crystal plays no role at all in determining C L . In this limiting case, it makes sense to refer to C L as the oscillator load capacitance as it is determined entirely by the oscillator. However, when it comes time to order crystals, one specifies crystals having frequency f at a load capacitance C L , i.e. it is a condition on the crystal’s frequency. Because of this,it would be reasonable to refer to C L as the crystal load capacitance. For the sake of argument, we simply avoid the issue and use the term loadcapacitance.
注释:1> When ordering crystals for series resonant operation,instead of specifying a value for C L , be sure to state that the frequency f refers to the series-resonant frequency, F s .
2> This is not to say that all aspects of frequency determination are tied to this single number. For example,other aspects of the crystal and oscillator determine whether the correct mode of oscillation is selected and the system’s frequency stability (short and long term).
3. Defining F L at C L
We now take Equation (1) as our defining relation for what we mean by a crystal having a given frequency at a given load capacitance.
Definition: A crystal has frequency F L at a load capacitance C L when the reactance X of the crystal at frequency F L is given by Equation (1), where now ω = 2πF L .
Recall that, around a given mode, the reactance of a crystal increases from negative values, through zero at series resonance, to large positive values near parallel resonance where it rapidly decreases to large negative values, and then again it increases towards zero. (See Reference [1].) By excluding a region around parallel resonance, we have a single frequency for each value of reactance. In this way,we can associate a frequency F L given a value of C L .So, positive values of C L correspond to a frequency between series and parallel resonance. Large negative values of C L , correspond to a frequency below series resonance while smaller negative values correspond to frequencies above parallel resonance.(See Equation (3) below.)
3.1. The crystal frequency equation So, how much does the frequency of oscillation depend on the load capacitance C L ? We can answer this question by determining how the crystal frequency F L depends on the crystal load capacitance CL . One can show that to a very good approximation that
where C 1 and C 0 are the motional and static capacitances of the crystal, respectively. (See Reference [1] for a derivation and discussion of this relation.) For the purposes of this note, we shall refer to Equation (3) as the crystal frequency equation.
This shows the dependence of a crystal oscillator’s operational frequency on its load capacitance and its dependence on the crystal itself. In particular, the fractional frequency change when changing the load capacitance from C L1 to C L2 is given to good approximation by
3.2. Trim sensitivity
Equation (3) gives the dependence of operating frequency F L on the load capacitance C L . The negative fractional rate of change of the frequency with C L is known as the trim sensitivity, TS. Using Equation (3), this is approximately
From this we see that the crystal is more sensitive to given change in C L at lower values of C L .
4. But what determines C L ?
Consider the simple Pierce oscillator consisting of a crystal, an amplifier, and gate and drain capacitors as shown in Figure 2.
There are at least three stray capacitances that must be considered in trying to calculate the load capacitance of the Pierce oscillator circuit.
1. An added capacitance from the input of the amplifier to ground. Sources for this could be the amplifier itself and trace capacitance to ground. As this capacitance is in parallel with C G , we can simply absorb this into our definition of C G . (That is C G is the capacitance of the capacitor to ground plus any additional capacitance to ground on this side of the amplifier.)
2. An added capacitance from the output of the amplifier to ground. Sources for this could be the amplifier itself and trace capacitance to ground. As this capacitance is in parallel with C D , we can simply absorb this into our definition of C D . (That is C D is the capacitance of the capacitor to ground plus any additional capacitance to ground on this side of the amplifier.)
3. A stray capacitance C s shunting the crystal as shown in Figure 2.
Redefining C G and C D as discussed above, it then follows [2] that one of the conditions for oscillation is
Where
is the impedance of the parallel combination of the crystal and the capacitance C s and R o is the output resistance of the amplifier.
It can be shown that the crystal resistance R as a function of load capacitance C L is given approximately by (provided C L is not too small)
where R 1 is the motional resistance of the crystal [1].It then follows that (provided C L – C s is not too small)
And
With these results, Equation (6) gives the following equation for C L
where R ′ is approximated by Equation (9). Note that the equation for C L is actually a bit more complicated than it might seem at first as R ′ depends upon on C L.It can be seen that C L decreases as R 1 increases, and so by Equation (3), the frequency of operation increases with crystal resistance. So, the load capacitance does have a dependence on the crystal itself. But as we have mentioned previously, the variation in crystal resistance and resulting sensitivity to this variation is usually sufficiently low that the dependence can be ignored. (In this case, a nominal value for crystal resistance is used in calculating C L .)
However, sometimes the resistance effect cannot be ignored. Two crystals tuned so that both have exactly the same frequency at a given load capacitance C L can oscillate at different frequencies in the same oscillator if their resistances differ. This slight difference leads to an increase in the observed system frequency variation above that due to crystal frequency calibration errors and the board-to-board component variation.
Note that in the case of zero crystal resistance (or at least negligible compared to the output resistance Ro of the amplifier), Equation (11) gives
So, in this case, the load capacitance is the stray capacitance shunting the crystal plus the series capacitance of the two capacitances on each side of the crystal to ground.
5. Measuring CL
While in principal one could calculate C L from the circuit design, an easier method is simply to measure C L . This is also more reliable since it does not rely on the oscillator circuit model, takes into account the strays associated the layout (which can be difficult to estimate), and it takes into account the effect of crystal resistance. Here are two methods for measuring C L .
5.1 Method 1
This method requires an impedance analyzer, but does not require knowledge of the crystal parameters and is independent of the crystal model.
1. Get a crystal that is similar to those that will be ordered, i.e. having similar frequency andresistance.
2. Place this crystal in the oscillator and measurethe frequency of operation F L . In placing the crystal into the circuit, be careful not to damage it or do anything to cause undue frequency shifts.(If soldered in place, allow it to cool down to room temperature.) A good technique that avoids soldering is simply to press the crystal onto the board’s solder pads using, for example,the eraser end of a pencil and observe the oscillation frequency. Just be careful that the crystal makes full contact with the board. The system can still oscillate at a somewhat higher frequency without the crystal making full contact with the board.
3. Using an impedance analyzer, measure the reactance X of the crystal at the frequency F L determined in Step 2.
4. Calculate C L using Equation (1) and the measured values for F L ( ω = 2πF L ) and X at F L .
5.2 Method 2
This method is dependent upon the four-parameter crystal model and requires knowledge of these parameters (through your own measurement or as provided by the crystal manufacturer).
1. Get a crystal that is similar to those that will be ordered, i.e. having similar frequency and resistance.
2. Characterize this crystal. In particular measure its series frequency Fs , motional capacitance C1,and static capacitance C0.
3. Place this crystal in the oscillator and measure the frequency of operation F L (as in Method 1,Step 2.)
4. Calculate C L using Equation (3) and the measured values for F L , F s , C 1 , and C 0 .
It is recommended that either procedure be followed with at least 3 crystals. When done properly, this technique often gives values for C L that are consistent to about 0.1 pF. Further confidence in the final results can be found by repeating the procedure for a number of boards to estimate the board-to-board variation of C L .
Note that in the above, F L does not have to be precisely the desired oscillation frequency f. That is, the calculated value for C L is not a strong function of the oscillation frequency since normally only the crystal is strongly frequency dependent. If, for some reason, the oscillator does have strong frequency dependent elements, then using this procedure would be quite difficult.
6. Do I really need to specify a value for CL ?
There are at least three cases where a specification of C L is not necessary:
1. You intend to operate the crystals at their series-resonant frequency.
2. You can tolerate large errors in frequency (on theorder of 0.1% or more).
3. The load capacitance of your circuit is sufficiently near the standard value (see crystal data sheet) that the frequency difference is tolerable. This difference can be calculated with Equation (4).
If your application does not meet one of the three conditions above, you should strongly consider estimating the load capacitance of your oscillator and use this value in specifying your crystals.
- 阅读(232)
相关搜索
热点聚焦
- 1时钟振荡器XO57CTECNA12M电信设备专用晶振
- 2汽车音响控制器专用晶振403C35D28M63636
- 3XCO时钟振荡器C04310-32.000-EXT-T-TR支持微控制器应用
- 4ABS07W-32.768KHZ-J-2-T音叉晶体可实现最佳的电路内性能
- 5402F24011CAR非常适合支持各种商业和工业应用
- 6无线模块专用微型ECS-240-8-36-TR晶体
- 7DSX321G晶体谐振器1N226000AA0G汽车电子控制板专用晶振
- 8lora模块低功耗温补晶振ECS-327TXO-33-TR
- 9ECS-250-12-33QZ-ADS-TR适合高冲击和高振动环境的理想选择
- 10ECS-200-20-20BM-TR紧凑型SMD晶体是物联网应用的理想选择
 泰河盛微信号
泰河盛微信号

 在线留言
在线留言 收藏网站
收藏网站 网站地图
网站地图
 手机版
手机版
 全球咨询热线:
全球咨询热线:
 快速通道
快速通道
